How Backpropagation Algorithm works?
The backpropagation algorithm is used in layered feed-forward ANNs.

Do you have similar website/ Product?
Show in this page just for only
$2 (for a month)

0/60
0/180
Artificial neurons are organized in layers,
and send their signals ?forward?, and then the errors are propagated backwards. The
network receives inputs by neurons in the input layer, and the output of the network is given
by the neurons on an output layer. There may be one or more intermediate hidden layers.
The backpropagation algorithm uses supervised learning, which means that we provide the
algorithm with examples of the inputs and outputs we want the network to compute, and
then the error is calculated. The idea of
the backpropagation algorithm is to reduce this error, until the ANN learns the training
data. The training begins with random weights, and the goal is to adjust them so that the
error will be minimal.
The activation function of the artificial neurons in ANNs implementing the
backpropagation algorithm is a weighted sum :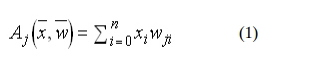
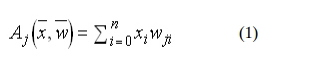
If the output function would be the identity (output=activation), then the neuron
would be called linear. But these have severe limitations. The most common output
function is the sigmoidal function: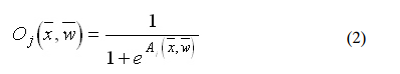 The sigmoidal function is very close to one for large positive numbers, 0.5 at zero,
and very close to zero for large negative numbers. This allows a smooth transition between
the low and high output of the neuron (close to zero or close to one). We can see that the
output depends only in the activation, which in turn depends on the values of the inputs and
their respective weights.
The sigmoidal function is very close to one for large positive numbers, 0.5 at zero,
and very close to zero for large negative numbers. This allows a smooth transition between
the low and high output of the neuron (close to zero or close to one). We can see that the
output depends only in the activation, which in turn depends on the values of the inputs and
their respective weights.
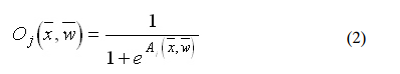
Now need to adjust the weights in order to
minimize the error. We can define the error function for the output of each neuron: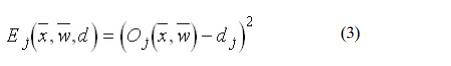
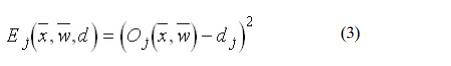
The error of the network will simply be the sum of the errors
of all the neurons in the output layer: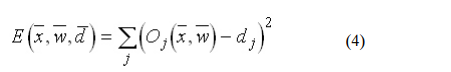
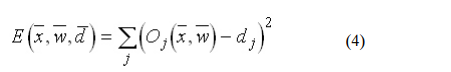
The backpropagation algorithm now calculates how the error depends on the
output, inputs, and weights. After we find this, we can adjust the weights using the method
of gradient descendent: Now we need to
calculate how much the error depends on the output, which is the derivative of E in respect
j
to O (from (3)).
Now we need to
calculate how much the error depends on the output, which is the derivative of E in respect
j
to O (from (3)). 


How much the output depends on the activation, which in turn depends
on the weights (from (1) and (2)):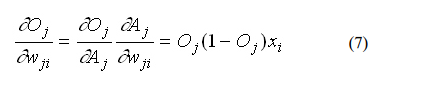
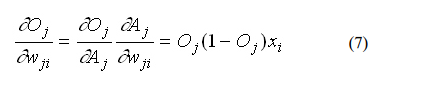
From (6) and (7)):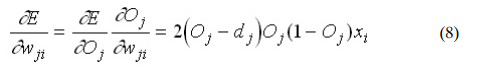
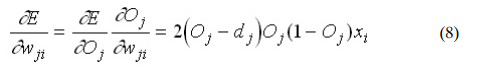
The adjustment to each weight will be (from (5) and (8)):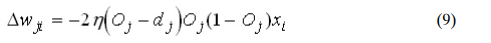
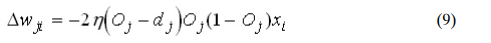
We can use (9) as it is for training an ANN with two layers. Now, for training the
network with one more layer we need to make some considerations. If we want to adjust
ik the weights (let?s call them v ) of a previous layer, we need first to calculate how the error
depends not on the weight, but in the input from the previous layer. This is easy, we would
i ji
just need to change x with w in (7), (8), and (9). But we also need to see how the error of
ik the network depends on the adjustment of v . So: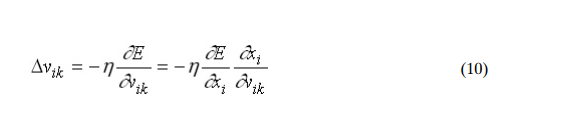
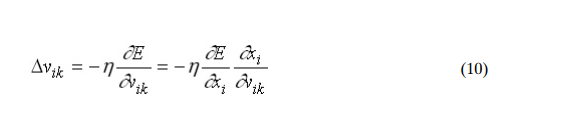
Where: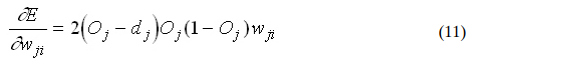 Assuming that there k ik
are inputs u into the neuron with v (from (7)):
Assuming that there k ik
are inputs u into the neuron with v (from (7)): If we want to add yet another layer, we can do the same, calculating how the error
depends on the inputs and weights of the first layer. We should just be careful with the
indexes, since each layer can have a different number of neurons, and we should not
confuse them.
For practical reasons, ANNs implementing the backpropagation algorithm do not
have too many layers, since the time for training the networks grows exponentially. Also,
there are refinements to the backpropagation algorithm which allow a faster learning.
If we want to add yet another layer, we can do the same, calculating how the error
depends on the inputs and weights of the first layer. We should just be careful with the
indexes, since each layer can have a different number of neurons, and we should not
confuse them.
For practical reasons, ANNs implementing the backpropagation algorithm do not
have too many layers, since the time for training the networks grows exponentially. Also,
there are refinements to the backpropagation algorithm which allow a faster learning.
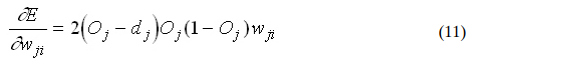

CONTINUE READING
ANNs
Ayesha
Tech writer at newsandstory
